A simple iterative model of population growth (and decline) over time is
x → μ x (1 − x)
We choose a value for the parameter μ and a starting x value, then repeatedly substitute the results of each mapping into x on the right-hand side of the mapping; the list of partial results can be viewed as a time series of the population levels over a discrete sequence of times.
For example, if we let μ be 2, and let x start with 0.25, the first few iterates are
{0.25, 0.375, 0.46875, 0.498047, 0.499992, 0.5, 0.5, 0.5, ...}.
Similarly, if we let μ be 2.5, the first few iterates are
{0.25, 0.46875, 0.622559, 0.587448, 0.605882, 0.596973, 0.601491, 0.599249, 0.600374, 0.599813, 0.600094, 0.599953, 0.600023, 0.599988, 0.600006, 0.599997, 0.600001, 0.599999, 0.6, 0.6, 0.6, ...}.
For values of μ between 1 and about 3, the iteration settles down to a single value.
If we let μ be 3.2, the list of iterates is
{0.25, 0.6, 0.768, 0.570163, 0.784247, ..., 0.799455, 0.513045, 0.799455, 0.513045, ...};
the iteration eventually oscillates forever between the two values 0.799455 and 0.513045. The iteration has period two for values of mu between 3 and about 3.4494.
If we choose μ = 3.46, the iterates are
{0.25, 0.64875, 0.788442, 0.577132, ..., 0.838952, 0.467486, 0.861342, 0.413234, 0.838952, ...},
where the last four values repeat forever, or fall into a period-4 cycle. The phenomenon of period-doubling for greater values of μ is called bifurcation.
For greater values of μ, the list of iterates is chaotic; the iteration does not settle down to a fixed point or cycle, but rather apparently behaves randomly.
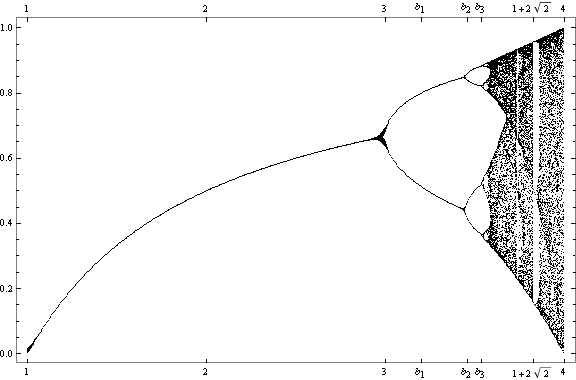
Here we visualize the iterations of the mapping for values of μ ranging from 2.4 to 3.8 in increments of 0.2. We see that for small values of μ the iteration settles down to a fixed point or a cycle, but that for larger values the behavior is chaotic.
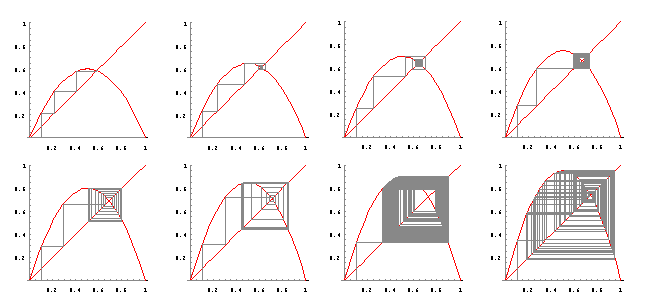
Designed and rendered using Mathematica 3.0 for the Apple Macintosh, with more than a little help from Peitgen et al, Chaos and Fractals, Springer-Verlag, 1992.
© 1997–2026 by Robert Dickau
[ home ] || [ 97???? ]
www.robertdickau.com/bifurcation.html