The Cantor set is a classical fractal generated by iteratively removing the middle third of a collection of line segments. To begin, start with a line segment from 0 to 1.
___________________________
Removing the middle third results in segments (0, 1/3) and (2/3, 1).
_________ _________
Removing the middle third of each of the remaining segments results in (0, 1/9), (2/9, 3/9), (6/9, 7/9), and (8/9, 1).
___ ___ ___ ___
And again:
_ _ _ _ _ _ _ _
The limit of this process is the Cantor set, which has Hausdorff dimension 0.6309.

Cantor dust is a two-dimensional fractal figure generated beginning with a square; with each iteration, remove the middle third horizontal and vertical stripe of each square in the figure. (Compare this process with the Sierpinski carpet process.)
The following figure shows the first few stages:

The Hausdorff dimension is 1.2619.
The same process can be carried out in three dimensions:
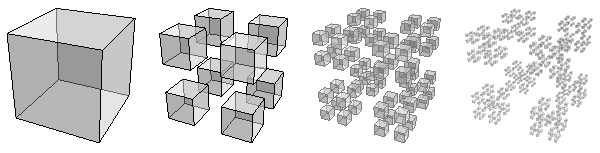
(Compare this process with the Menger sponge generation process.)
Designed and rendered using Mathematica 2.2 for the Apple Macintosh and (much, much later) 7.0 for Microsoft Windows.
© 1996–2026 Robert Dickau
[ home ] || [ 2014-05-17 ]
www.robertdickau.com/cantor.html