
Delannoy numbers describe the number of paths from the southwest corner of a rectangular grid to the northeast corner, using only single steps north, northeast, or east. Delannoy numbers can be computed recursively using this formula:
D(a, b) = D(a−1, b) + D(a, b−1) + D(a−1, b−1) [Weisstein 1999],
where D(0, 0) = 1.
For a 1 × 1 grid, there are 3 paths:

For a 2 × 2 grid, there are 13 paths:
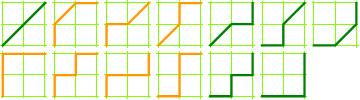
3 × 3 grid, 63 paths:

The Delannoy paths that do not rise above the SW–NE diagonal (the paths drawn above in green) represent the Schröder numbers.
Another interpretation of the Schröder numbers is the number of ways a rectangle containing n points—with no two points falling on a line parallel to the rectangle’s edges—can be sliced into smaller rectangles, where each slice intersects one of the points, is parallel to one of the rectangle’s edges, and divides only a single rectangle.
1 slice, 2 ways:
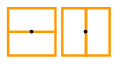
2 slices, 6 ways:

3 slices, 22 ways:

4 slices, 90 ways:
You might enjoy the 3D extension, Schröder 3D Rectangulations (3D Guillotine Partitions).
See also “Schröder Rectangulations” at the Wolfram Demonstrations Project.
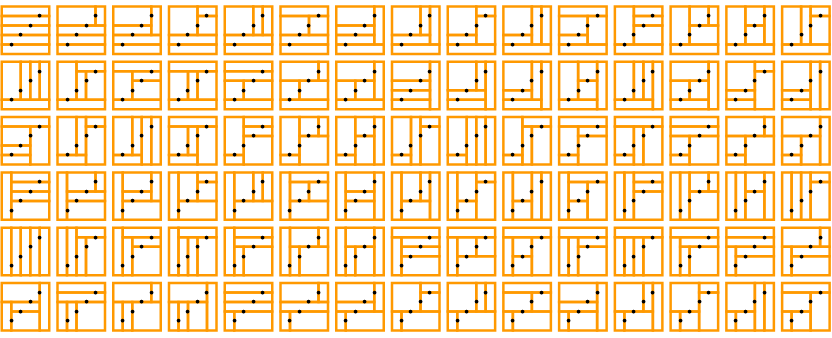
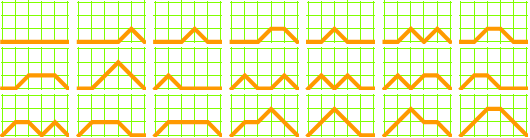
The Motzkin numbers describe the number of paths from the southwest corner of a grid to the southeast corner, using only steps northeast, east, and southeast. (Clearly, for a grid with width n the maximum necessary height is ⌊n/2⌋.)
2 × 2 grid, 2 paths:
3 × 3 grid, 4 paths:
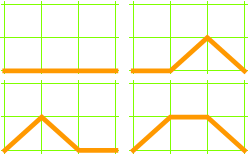
4 × 4 grid, 9 paths:
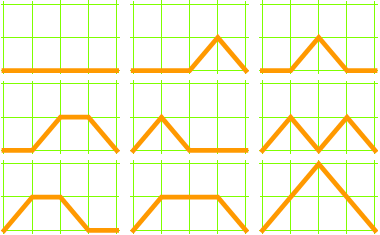
5 × 5 grid, 21 paths:
Definitions and formulas cribbed from Eric Weisstein’s CRC Concise Encyclopedia of Mathematics (CRC Press, 1999), pp. 411 and 1201.
Figures originally designed and rendered using Mathematica.
You might also enjoy Counting Lattice Paths.
© 1999–2026 Robert Dickau.
[ home ] || [ 2008-03-31 ]
www.robertdickau.com/delannoy.html