Derangements

A derangement (or complete permutation) of a set is a permutation that leaves no element in its original position. The number of derangements of a set with n elements can be computed recursively using this formula:

D(n + 1) = n (D(n) + D(n–1))

Using the principle of inclusion and exclusion, we also get:

Here are some diagrams that represent the derangements of sets with n elements.

3 elements, 2 derangements:

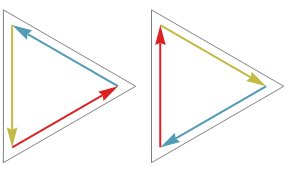
4 elements, 9 derangements:

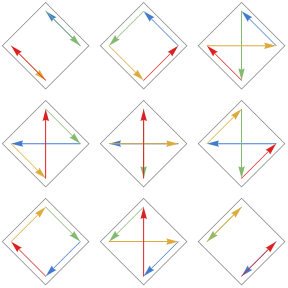
5 elements, 44 derangements:

The counts are also known as subfactorials, with notation !n.

Derangements also count n×n chessboards with n non-attacking rooks that avoid the main (NW–SE) diagonal.

D₃ = 2:

D₄ = 9:

D₅ = 44:

Derangement formulas from Fred S. Roberts, Applied Combinatorics, Prentice-Hall, 1984.

Designed and rendered on various weekends over the years using Mathematica versions 3.0, 6.0, 7.0, and 13.2.

© 1996–2023 by Robert Dickau.

[ home ] || [ 2023-02-11 ]