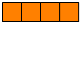
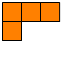

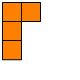
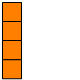
An integer partition is just what it sounds like: a way to split a positive integer n into a set of smaller positive integers that add up to n. For example, 4 can be partitioned in a few different ways:
The order of the parts doesn’t matter. By convention, the elements of the partition are sorted from greatest to least.
One representation of an integer partition is as a Ferrers board. In a Ferrers board, each integer in a partition is represented as a row of that many boxes—3 is represented by a row of 3 boxes—with each part of the partition placed in a different row.
So the Ferrers boards for the different partitions of 4 look like this:
| 4: |  |
| 3 + 1: | 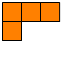 |
| 2 + 2: |  |
| 2 + 1 + 1: | 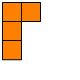 |
| 1 + 1 + 1 + 1: |  |
(Sometimes you’ll hear this kind of diagram, or this kind of diagram flipped vertically, called a Young diagram, not to be confused with a Young tableau, which has numbers in the boxes. I don’t really understand the difference, myself. While we’re at it, a Ferrers diagram, as opposed to Ferrers board, is similar but consists of dots instead of boxes.)
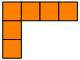
Ferrers boards are useful for proving various identities about partitions. For example, a Ferrers board for a partition can be interpreted as a different partition by reading columns instead of rows. Take this board:
The standard interpretation, reading by rows, is 3 + 2:
But reading it by columns gives us 2 + 2 + 1.
Partitions related in this way are called conjugate partitions.
In general, if an integer’s partition into k parts has greatest part m, in one board interpretation there are k rows, the longest of which has m boxes; and in the other interpretation has m columns, the longest of which has k boxes. These two interpretations can then be translated into an identity to the effect of “An integer n can be partitioned into m parts in the same number of ways it can be partitioned so that its greatest part is m.” Likewise for k.
Another interpretation based on Ferrers boards is, “The number of partitions of n is the same as the number of paths through an n × n lattice, starting at the southwest corner and ending at the northeast corner, taking only steps north and east, for which there are n boxes above and to the left of the path.”
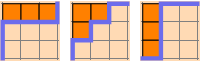
Ferrers boards can be partially ordered based on whether one board fits inside another one. For example, this board:
is “less than” this board:

but not this one:
The following is a Hasse diagram of the partitions of 1 through 7, where an arrow connects a Ferrers board to all of the boards that can be created by adding a single box to it:
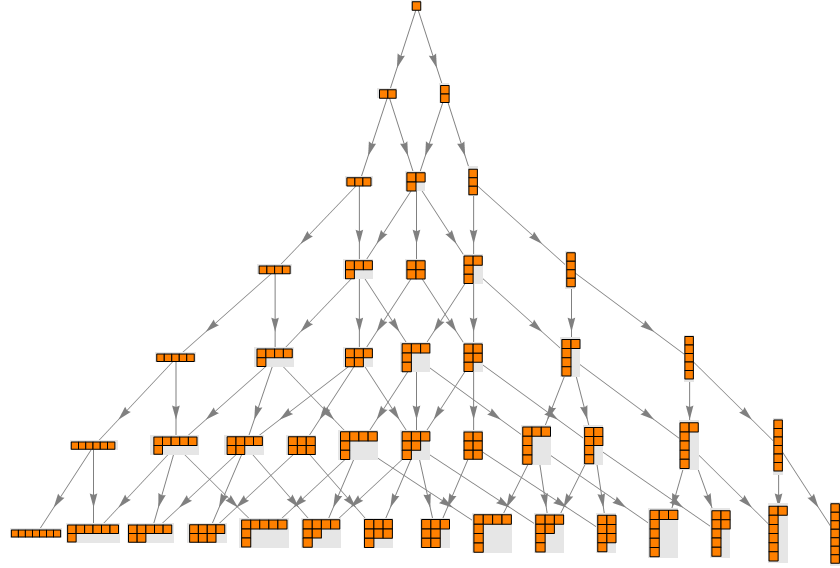
I guess it’s really an upside-down Hasse diagram. Call the whole thing a lattice if that’s a problem.
See G. E. Andrews and K. Eriksson, Integer Partitions, Cambridge: Cambridge University Press, 2004, especially p. 108.
Designed and rendered using Mathematica 7.0. Embarrassingly, I noticed only later that Mathematica 6 had added a built-in IntegerPartitions function, which might have saved some trouble.
© 2012–2026 by Robert Dickau.
[ home ] || [ 2012-12-24 ]