{6,2,1,0,0,0,1,0,0,0} lists its own count of each digit 0–9.{7,1,0,1,0,0,1,0,0,0} and {6,3,0,0,0,0,0,1,0,0}
list each other’s counts of each digit 0–9.While searching for the last sentence, I was hoping there would be some striking correlations among the simultaneous counts of letters—say, t’s, e’s, and n’s—as the iteration went along (something like the Lozi attractor, perhaps), but it doesn’t look like it.
For what it’s worth:
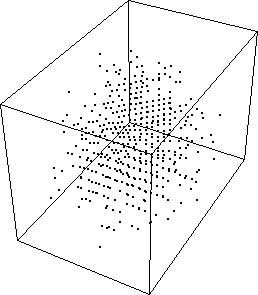
Plot of t vs. e vs. n:
Plots of e-vs.-t, e-vs.-n, and t-vs.-n:
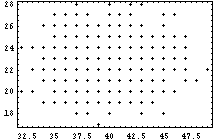
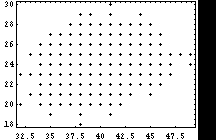
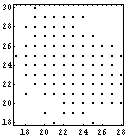
From one successful search that took 807 iterations:
| e | t | n | |
|---|---|---|---|
| Final | 39 | 25 | 22 |
| Mean | 39.97 | 22.56 | 23.76 |
| Variance | 8.17 | 3.59 | 4.01 |
See, of course, Hofstadter, D. R., Metamagical Themas; Chapter 2, “Self-Referential Sentences: A Follow-Up”, and Chapter 16, “Mathematical Chaos and Strange Attractors”; Basic Books, New York, 1985.
© 1998 Robert Dickau.
[ home ] || [ 1998-02-02 ]
www.robertdickau.com/filename.html