In combinatorics, a stacking of coins such that any coin above the bottom row must rest on two coins in the row below it is sometimes called a fountain. Different ways of counting fountains are to group them by the width of the base, or by the total number of coins.
Grouping them by the width of the base, there’s only one fountain—if you can call it that—with a base 1 coin wide. A fountain with n coins and a base k coins wide is sometimes called an (n, k) fountain. The following would be a (1, 1) fountain.

There are two fountains that have a base 2 coins wide.
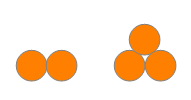
There are five fountains that have a base 3 coins wide. As you can see, the maximum number of coins in a fountain with a base n coins wide is n(n+1)/2, the nth triangular number Tn. The minimum is when the base is the whole fountain, of course.

There are 14 fountains with a base 4 coins wide.
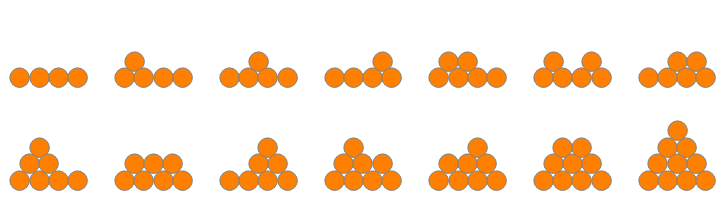
There are 42 fountains with a base 5 coins wide.

As it turns out, these are the Catalan numbers. This follows by matching each fountain with a given base width to a lattice path with a given number of steps.
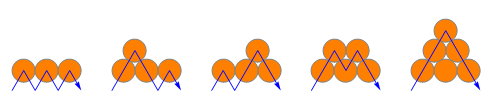
The other way to group them is by the number of coins in the entire fountain, not just the base. A fountain with n coins is sometimes called an n-fountain. The only fountain with a total of one coin is, well, one coin (●), and the only fountain with two coins is just two coins next to each other (●●).
There are two fountains made out of 3 coins.

There are three fountains made out of 4 coins.

There are five fountains made out of 5 coins.

There are nine fountains made out of 6 coins.
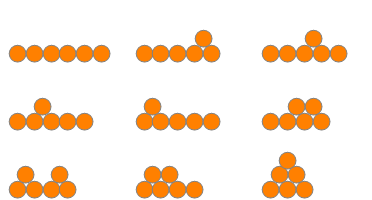
There are 15 fountains made out of 7 coins.
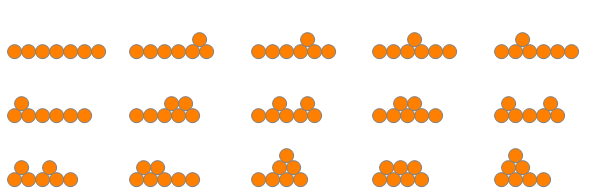
There are 26 fountains made out of 8 coins.

Skipping ahead a bit, there are 78 fountains made out of 10 coins, starting and ending with these:

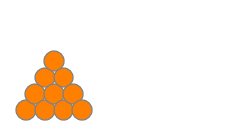
This is OEIS sequence A005169.
See R. P. Stanley, Enumerative Combinatorics, Volume 2, Cambridge: Cambridge University Press, 1999, p. 228 (it’s part hhh of that famous Exercise 6-19); and S. R. Finch, Mathematical Constants, Cambridge: Cambridge University Press, 2003, pp. 380–1.
© 2011–2025 by Robert Dickau.
[ home ] || [ 2012-03-31 ]