As you’ve seen, Catalan numbers have many interpretations in combinatorics, including:
A generalization of Catalan numbers uses triples instead of pairs, for example:
The sequence of numbers described by this generalization is called the Fuss–Catalan numbers, with values:
You’ll sometimes see this notation:
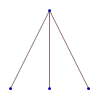
There’s one way to parenthesize {1, 2, 3} as a triple (specifically, leave it alone):
{1, 2, 3}
One planar ternary tree with three leaves:
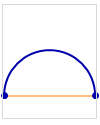
One path from (0, 0) to (2, 1) that doesn’t cross above the diagonal:

One partition of {1, 2} into subsets of even size:
And one way to cut a square into one quadrilateral (with zero cuts):
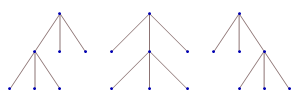
Three ways to parenthesize {1, 2, 3, 4, 5} as triples:
{{1, 2, 3}, 4, 5}
{1, {2, 3, 4}, 5}
{1, 2, {3, 4, 5}}
Three corresponding planar ternary trees:
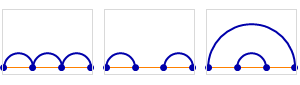
Three paths from (0, 0) to (4, 2) that don’t cross above the diagonal:

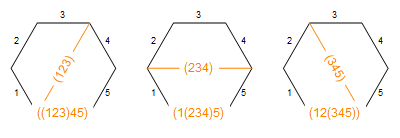
Three non-crossing partitions of {1, 2, 3, 4} into subsets of even size:
And three correponding ways to slice a hexagon into quadrilaterals (with one cut):
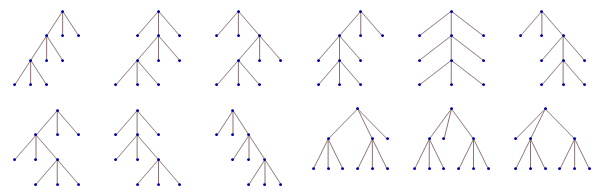
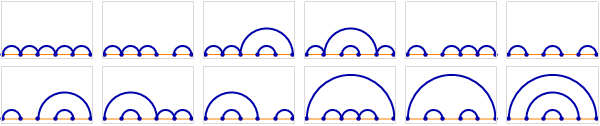
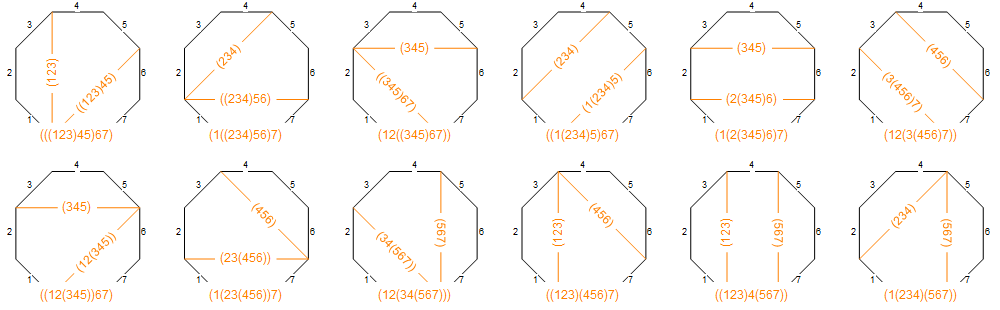
Twelve ways to parenthesize {1, 2, 3, 4, 5, 6, 7} as triples:
{{{1, 2, 3}, 4, 5}, 6, 7}
{1, {{2, 3, 4}, 5, 6}, 7}
{1, 2, {{3, 4, 5}, 6, 7}}
{{1, {2, 3, 4}, 5}, 6, 7}
{1, {2, {3, 4, 5}, 6}, 7}
{1, 2, {3, {4, 5, 6}, 7}}
{{1, 2, {3, 4, 5}}, 6, 7}
{1, {2, 3, {4, 5, 6}}, 7}
{1, 2, {3, 4, {5, 6, 7}}}
{{1, 2, 3}, {4, 5, 6}, 7}
{{1, 2, 3}, 4, {5, 6, 7}}
{1, {2, 3, 4}, {5, 6, 7}}
Twelve ternary trees:
Twelve paths from (0, 0) to (6, 3) that don’t cross above the diagonal:

Twelve non-crossing partitions of {1, 2, 3, 4, 5, 6} into subsets of even size:
And twelve ways to slice an octagon into quadrilaterals (with two cuts):
Fifty-five ways to parenthesize {1, 2, 3, …, 9}:
{{{{1,2,3},4,5},6,7},8,9} {1,{{{2,3,4},5,6},7,8},9} {1,2,{{{3,4,5},6,7},8,9}} {{1,{{2,3,4},5,6},7},8,9} {1,{2,{{3,4,5},6,7},8},9}
{1,2,{3,{{4,5,6},7,8},9}} {{1,2,{{3,4,5},6,7}},8,9} {1,{2,3,{{4,5,6},7,8}},9} {1,2,{3,4,{{5,6,7},8,9}}} {{{1,{2,3,4},5},6,7},8,9}
{1,{{2,{3,4,5},6},7,8},9} {1,2,{{3,{4,5,6},7},8,9}} {{1,{2,{3,4,5},6},7},8,9} {1,{2,{3,{4,5,6},7},8},9} {1,2,{3,{4,{5,6,7},8},9}}
{{1,2,{3,{4,5,6},7}},8,9} {1,{2,3,{4,{5,6,7},8}},9} {1,2,{3,4,{5,{6,7,8},9}}} {{{1,2,{3,4,5}},6,7},8,9} {1,{{2,3,{4,5,6}},7,8},9}
{1,2,{{3,4,{5,6,7}},8,9}} {{1,{2,3,{4,5,6}},7},8,9} {1,{2,{3,4,{5,6,7}},8},9} {1,2,{3,{4,5,{6,7,8}},9}} {{1,2,{3,4,{5,6,7}}},8,9}
{1,{2,3,{4,5,{6,7,8}}},9} {1,2,{3,4,{5,6,{7,8,9}}}} {{{1,2,3},{4,5,6},7},8,9} {1,{{2,3,4},{5,6,7},8},9} {1,2,{{3,4,5},{6,7,8},9}}
{{{1,2,3},4,{5,6,7}},8,9} {1,{{2,3,4},5,{6,7,8}},9} {1,2,{{3,4,5},6,{7,8,9}}} {{1,{2,3,4},{5,6,7}},8,9} {1,{2,{3,4,5},{6,7,8}},9}
{1,2,{3,{4,5,6},{7,8,9}}} {{{1,2,3},4,5},{6,7,8},9} {{{1,2,3},4,5},6,{7,8,9}} {{1,2,3},{{4,5,6},7,8},9} {{1,2,3},4,{{5,6,7},8,9}}
{1,{{2,3,4},5,6},{7,8,9}} {1,{2,3,4},{{5,6,7},8,9}} {{1,{2,3,4},5},{6,7,8},9} {{1,{2,3,4},5},6,{7,8,9}} {{1,2,3},{4,{5,6,7},8},9}
{{1,2,3},4,{5,{6,7,8},9}} {1,{2,{3,4,5},6},{7,8,9}} {1,{2,3,4},{5,{6,7,8},9}} {{1,2,{3,4,5}},{6,7,8},9} {{1,2,{3,4,5}},6,{7,8,9}}
{{1,2,3},{4,5,{6,7,8}},9} {{1,2,3},4,{5,6,{7,8,9}}} {1,{2,3,{4,5,6}},{7,8,9}} {1,{2,3,4},{5,6,{7,8,9}}} {{1,2,3},{4,5,6},{7,8,9}}
Fifty-five ternary trees:
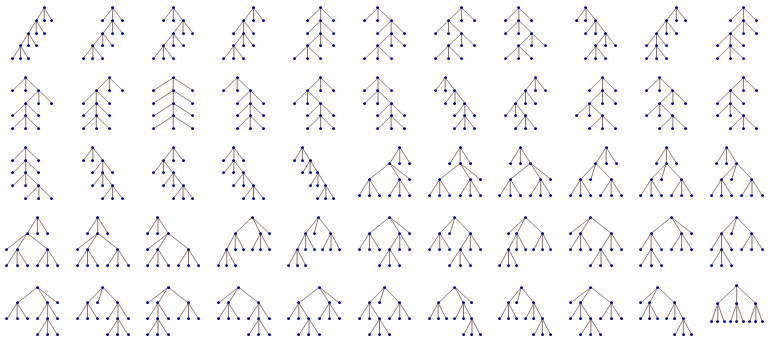
Fifty-five paths:
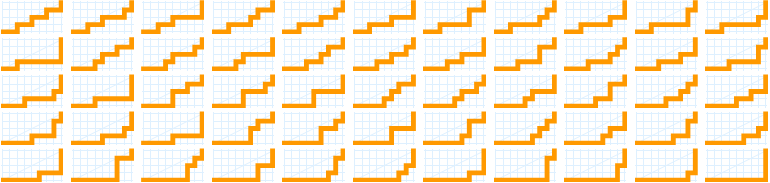
Fifty-five non-crossing partitions of {1, 2, 3, 4, 5, 6, 7, 8} into subsets of even size:

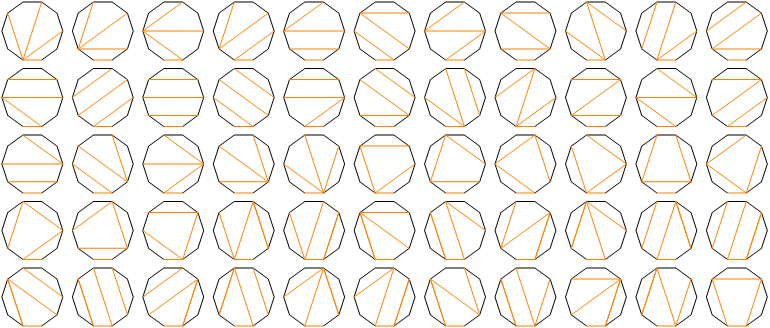
And 55 ways to slice a decagon into quadrilaterals:
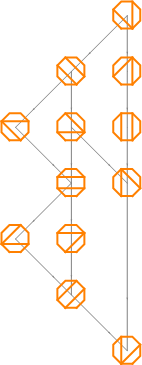
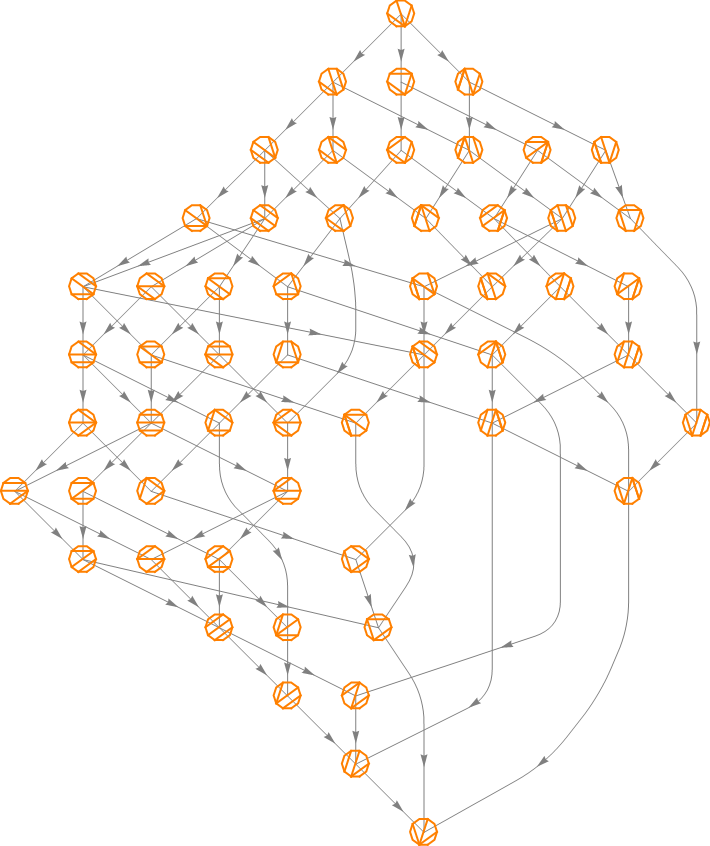
Just as the Catalan partitions can be partially ordered, the Fuss–Catalan partitions can be too. Here are some Tamari lattice–like partial orderings.


This sequence—1, 1, 3, 12, 55, 273, 1428, 7752, 43263, …—is OEIS sequence A001764.
See R. P. Stanley, Enumerative Combinatorics Volume 2, Cambridge University Press, 1999, pp. 212, 234 (Exercise 6.33(c)); and Graham, Knuth, and Patashnik, Concrete Mathematics: A Foundation for Computer Science, Addison-Wesley, 1994, p. 361.
See also Martin Gardner, Time Travel and Other Mathematical Bewilderments, Chapter 20, W. H. Freeman, 1988.
Figures created with Wolfram Mathematica 11.
Robert Dickau, 2016–2026.
[ home ] || [ 2016-09-24 ]
robertdickau.com/fusscatalan.html