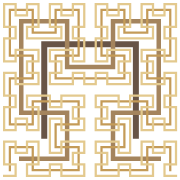
As I was saying, the plane-filling Hilbert curve (here shown with the first four iterations superimposed)—

—has a close relative called the Moore curve:

One difference being that the start and end points are adjacent corners of the square in the Hilbert curve, and adjacent points in the Moore curve.
And just as the Hilbert curve can be extended to a 3-D space-filling curve (here with the first three iterations intertwined)—
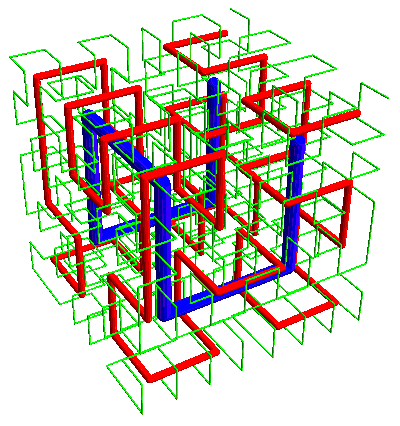
—the Moore curve can be extended:
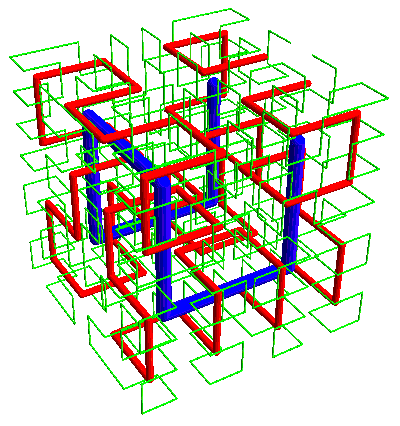
(Yes, I’m looking for a less awful color scheme that still shows contrast between the curves.)
Again, in the Hilbert curve the start and end are adjacent corners of the cube, while in the Moore case the ends are adjacent points.
Of course, there’s nothing that says the start and end points need to be on an outer edge of the square or cube. Other variations are possible by rotating the translated smaller squares or cubes, just as long as the end of one sub-curve can reach the beginning of the next one.
Figures created with Mathematica 6.
© 2008–2026 Robert Dickau.
[ home ] || [ 2008-07-06 ]
www.robertdickau.com/hilbert3d.html