There are at least a couple of 2-D curves called Koch curves, or sometimes von Koch curves. The reason I bring it up is, there are also a few 3-D variations called Koch surfaces.
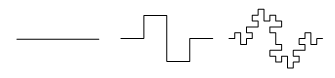
First, there’s what’s usually called the Koch curve or von Koch curve:
![]()
The 3-D version starts with a triangle, then builds a tetrahedron based on the midpoints of the triangles in the previous iteration:
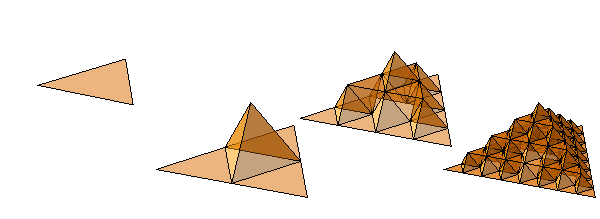
[Director's commentary: It seems as if deeper iterations should involve smaller tetrahedra, just as the 2-D version above has smaller triangles, and just as the quadratic versions below have smaller squares and cubes, but no obvious scaling ratio jumps out. I'm kind of busy right now, but let's sleep on it. Watch this space.]
Then there are at least a couple of 2-D curves called quadratic Koch curves. This version is similar to the triangle version above, using squares (minus a side) instead of equilateral triangles (minus a side) at each step.
![]()
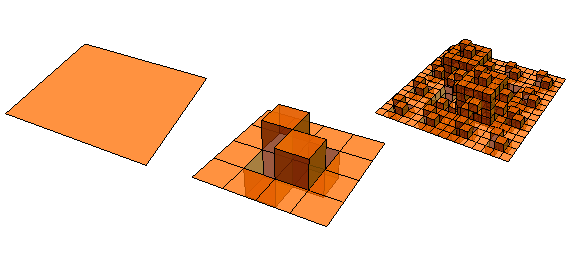
The 3-D variation of this type starts with a square, then builds up a cube on the middle ninth of each square of the previous iteration:

Another variation of the quadratic Koch curve, sometimes called a 3/2 curve, forms squares above and below the baseline.
The 3-D variation also starts with a square, then extends cubes above and below in a diagonal pattern. Kind of hard to describe:
A larger figure for iteration 3:

Some terminology and notes from Hans Sagan, Space-Filling Curves, Universitext, 1994, throughout.
Designed and rendered using Mathematica 7.0 and (much, much later, it seems) 10.0 for Microsoft Windows.
© 2008–2026 Robert Dickau.
[ home ] || [ 2015-05-24 ]
www.robertdickau.com/kochsurface.html