Here are some diagrams that represent the possible paths of length 2n from one corner of an n-by-n grid to the opposite corner. The number of paths are the central binomial coefficients
![]() or
or
![]() ,
,
central meaning they fall along the center line of Pascal’s triangle.
One reason this makes sense is that all of the paths in the figures below consist
of n steps east and n steps north, so from the 2n steps we
choose n, giving
![]() .
.
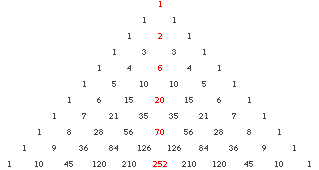
You can also use the old trick of numbering the possible ways to get to each point, which gives you Pascal’s triangle turned on its side. The numbers on the diagonal connecting the start and end points—1, 2, 6, and 20, in the figure below—are the central binomial coefficients:

(The Catalan numbers describe how many of these paths stay under the diagonal connecting the start and end points.)
1 × 1 grid, 2 paths:
![[ 1 x 1 (sorry, but the pictures speak a thousand words) ]](manhattan1.png)
2 × 2 grid, 6 paths:
![[ 2 x 2 ]](manhattan2.png)
3 × 3 grid, 20 paths:
![[ 3 x 3 ]](manhattan3.png)
4 × 4 grid, 70 paths:
![[ 4 x 4 ]](manhattan4.png)
Designed and rendered using Mathematica 3.0 for the Apple Macintosh and (much later) Mathematica 7.0 for Microsoft Windows.
© 1996–2026 by Robert Dickau.
[ home ] || [ 2010-12-29 ]