The Narayana numbers N(n, k) describe, among other things, the number of paths from (0, 0) to (2n, 0) that stay above the x-axis, using only steps northeast and southeast, having k peaks.
For example, N(1, 1) = 1, since there’s only one such path and it has one peak:
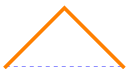
Likewise, N(2, 1) = 1 and N(2, 2) = 1, since there are two paths from (0, 0) to (4, 0); the first has one peak and the second has two peaks:
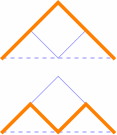
Here, N(3, 1) = 1; N(3, 2) = 3 [that is, there are three paths that have 2 peaks]; and N(3, 3) = 1.
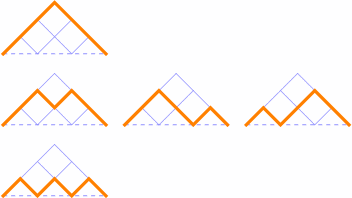
Paths for N(4, k):
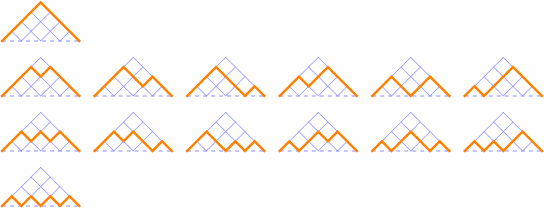
From these, we see that N(n, 1) = 1 and N(n, n) = 1.
The totals of N(n, k) as k goes from 1 to n are the Catalan numbers, as is apparent from the path interpretation.
© 1998–2026 by Robert Dickau.
[ home ] || [ 2011-02-20 ]