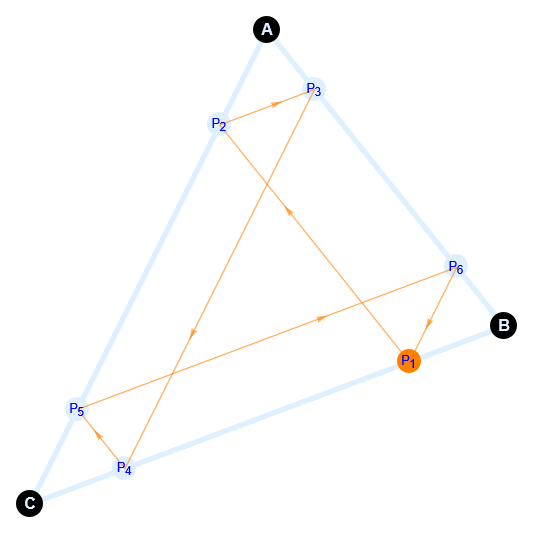
Thomsen’s figure, or Thomsen’s theorem, illustrates the following process: For any triangle ABC, pick a point P1 on BC opposite A. From P1 draw a line segment parallel to AB intersecting AC at point P2; then from there a segment parallel to BC intersecting AB at P3; continuing through the figure. Thomsen’s theorem shows that the final segment from P6 parallel to AC meets at the original point P1.

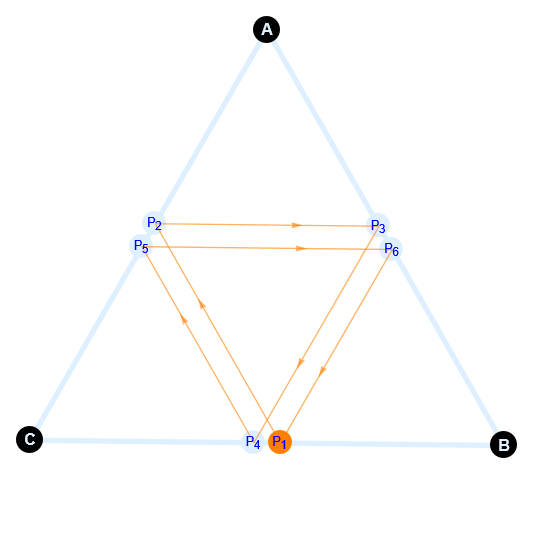
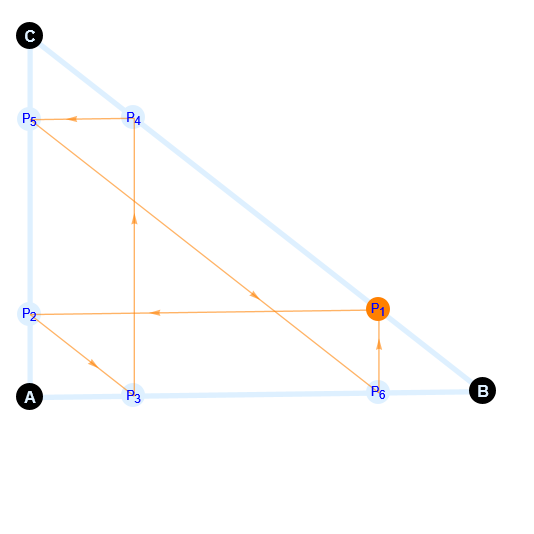
You might enjoy this interactive Wolfram Demonstrations Project version.
Should this work for any convex polygon with an odd number of sides? The arrows here aren’t parallel to the opposite sides, so not the right process.
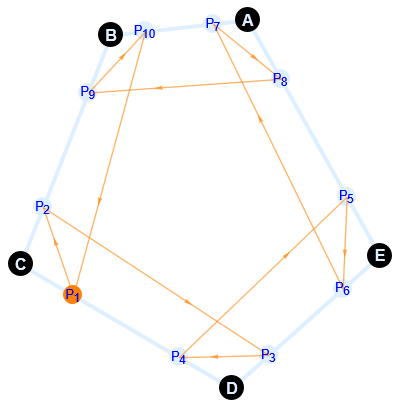
See:
Designed and rendered using Wolfram Mathematica 13.
First draft December 2021 by Robert Dickau.
[ home ] || [ 2023-02-10 ]