The Bell numbers (1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, ...) describe the number of ways a set with n elements can be partitioned into disjoint, non-empty subsets.
For example, the set {1, 2, 3} can be partitioned in the following ways:
{{1}, {2}, {3}}
{{1, 2}, {3}}
{{1, 3}, {2}}
{{1}, {2, 3}}
{{1, 2, 3}}
The nth Bell number can be computed using the formula:
where:
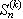
are the Stirling numbers of the second kind.
Here are some diagrams representing the different ways the sets can be partitioned: a line connects elements in the same subset, and a point represents a singleton subset.
{1, 2, 3}, 5 partitions:
{1, 2, 3, 4}, 15 partitions:

{1, 2, 3, 4, 5}, 52 partitions:

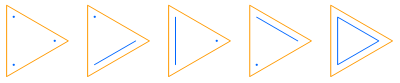
Partitions can be partially ordered by refinement. A partition π1 is a refinement of partition π2 if every part of π1 fits inside a partition of π2. Thus {{A},{B},{C}} is a refinement of {{A,B},{C}}, but {{A},{B,C}} isn’t since the {B,C} part doesn’t fit inside any single part of {{A,B},{C}}. If you break a chocolate bar into two pieces, and then break one of those pieces into two more pieces, the second partition is a refinement of the first.
This figure shows the lattice formed by the partitions of {A, B, C}:
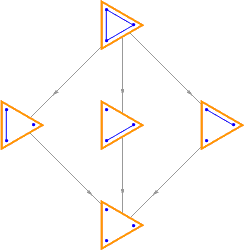
Lattice formed by the partitions of {A, B, C, D}:
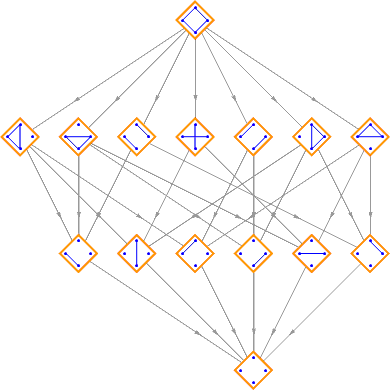
And the partitions of {A, B, C, D, E}:
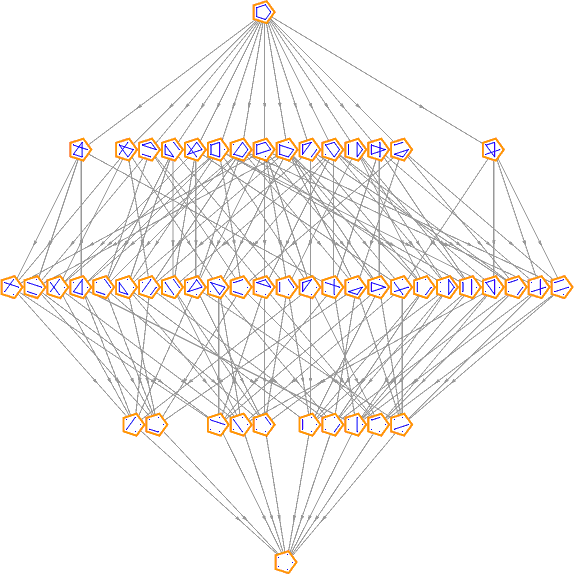
Each of the rows corresponds to the Stirling numbers of the second kind.
You might also enjoy this beautiful gallery of artistic interpretations: http://hermay.org/jconstant/bell/bellgallery/index.html
Designed and rendered using Mathematica 3.0 and (much, much later) 7.0.
© 1996–2026 by Robert Dickau.
[ home ] || [ 2011-05-22 ]