As you know, the factorial of \(n\)—written \(n\)!—is the product \(n \times (n-1) \times (n-2) \times \cdots \times 1\). The double factorial of \(n\)—written \(n!!\)—is the product \(n \times (n-2) \times (n-4) \times \cdots\), down to 1 if \(n\) is odd or 2 if \(n\) is even. So \(5!! = 5 \times 3 \times 1 = 15\), and \(6!! = 6 \times 4 \times 2 = 48\).
I was as surprised as anyone to learn that the double factorial isn’t \(n\) factorial factorial, \((n!)!\). To say nothing of the subfactorial \(!n\).
Double factorials figure into the counts of Stirling permutations. Stirling permutations are permutations of \(1,1,2,2,\dots,k,k\) where, for each \(i\), the two copies of \(i\) are adjacent or separated only by larger numbers. For example, the Stirling permutations of {1,1,2,2} are those where no 1 appears between the 2s. The permutations of {1,1,2,2} are:
Of these, {1,1,2,2}, {1,2,2,1}, and {2,2,1,1} meet the condition. The rest of them, {1,2,1,2}, {2,1,1,2}, and {2,1,2,1}, all have at least one 1 between the pair of 2s.
Similarly, {1,1,2,2,3,3}, {1,1,2,3,3,2}, {1,3,3,2,2,1}, are examples that meet the condition, but {3,2,2,3,1,1}, {1,2,3,1,2,3}, and {1,2,3,2,3,1} and others are not.
Stirling permutations are counted by \((2k-1)!!\).
One way to visualize Stirling permutations is as a simple list plot. The \((2\times 2 - 1)!! = 3!! = 3\) Stirling permutations of {1,1,2,2}:
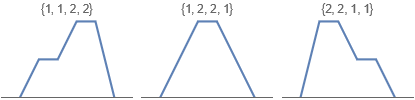
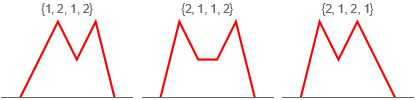
The permutations that don’t meet the Stirling permutation condition have sharp peaks:
The 5!! = 15 Stirling permutations of {1,1,2,2,3,3}:
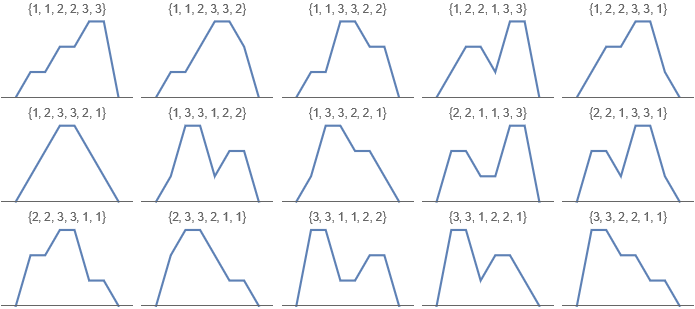
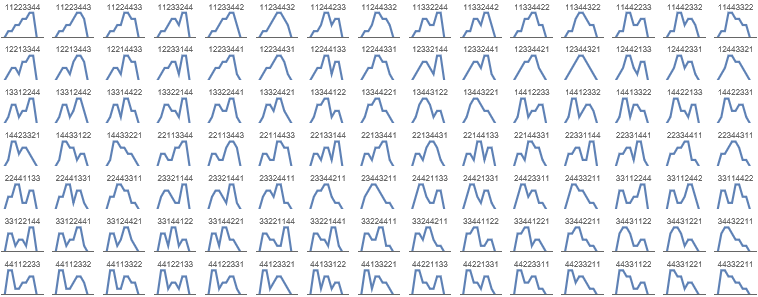
The 7!! = 105 Stirling permutations of {1,1,2,2,3,3,4,4}:
And the 9!! = 945 Stirling permutations of {1,1,2,2,3,3,4,4,5,5}:
Likewise, can visualize double factorials as \((2k-1)!!\) chord diagrams (aka perfect matchings) on complete graph \(K_{2k}\). The 3!! = 3 chord diagrams of complete graph \(K_4\):
The 5!! = 15 chord diagrams of \(K_6\):
And the 7!! = 105 chord diagrams of \(K_8\):
See:
[ home ] || [ 2026-05-04 ]