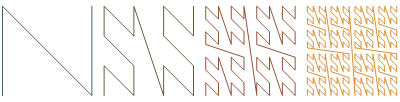
Similar to how the 2D Lebesgue curve is constructed—

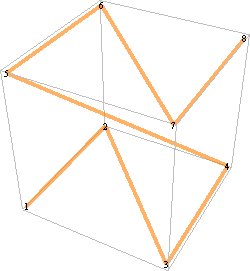
—a 3-D, non-self-intersecting, space-filling version can be constructed. Begin with the eight corners of a cube connected in the following order:
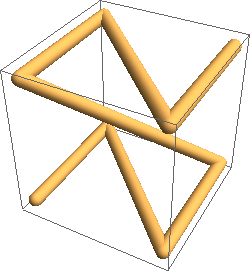
(Ignore the thickness of the lines; that’s just there to show perspective.)
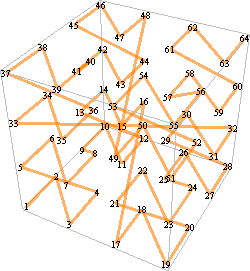
Each subsequent iteration is created by copying the entire figure to each corner of the cube, and then connecting the last point of each copy of the figure to the first point of the next copy. The last figure has exaggerated translations between iterations and a crazy color scheme to try to show how it’s put together.



The curve defines a mapping between the (one-dimensional) integers 1 through 8n, and three-dimensional integer coordinates in the cube with side 2n–1:

Figures created with Mathematica 6.
© 2009–2026 Robert Dickau.
[ home ] || [ 2008-05-03 ]
www.robertdickau.com/lebesgue3d.html