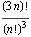
Here are some diagrams that represent the possible paths of length 3n from one corner of an n-by-n-by-n lattice to the opposite corner. The number of paths can be calculated using the formula:
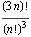
The first few terms are 1, 6, 90, 1680, 34650, 756756, 17153136, 399072960, ..., which are elements of the de Bruijn (3, n) sequence.
As with the 2-D version of the same idea, the numbers can be calculated by adding the number of possible paths to each point, step by step. The numbers are similar what would be “central” numbers in a 3-D analog to Pascal’s triangle.
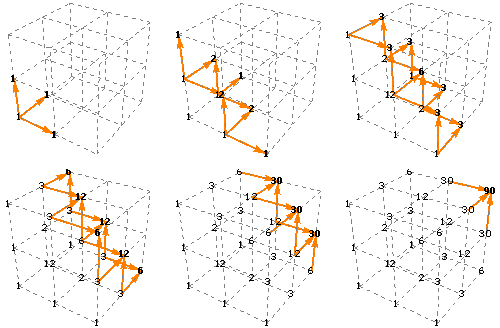
(Unsurprisingly, each face of the lattice has the same counts as the numbers of paths through a square lattice.)
1 × 1 × 1 lattice, 6 paths:

2 × 2 × 2 lattice, 90 paths:

Designed and rendered using Mathematica 3.0 for the Apple Macintosh and (much later) 7.0 for Windows.
(With thanks to Steven C. Fairgrieve for the information on the de Bruijn sequence.)
© 1994–2026 by Robert Dickau.
[ home ] || [ 2010-12-26 ]