Start with a cube.

If you slice off a corner of the cube, the exposed surface from the cut is a triangle. No surprise there.

If you make a deeper diagonal slice that intersects all of the cube’s faces, the exposed surface is a hexagon. Also not much of a surprise.
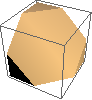
Now start again with the first iteration of the Menger sponge.

If you slice off a corner but miss the square holes, the exposed surface is still a triangle.

But if you make the slice deeper, the exposed hexagon surface contains a star-shaped hole. That is a surprise.

To help see why this happens, consider the inverse of the Menger sponge.
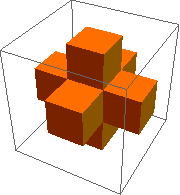
Draw dashed lines where the diagonal slice will go. You can kind of see that the cubes making up the arms of the shape will alternate between having the top front corner sliced off and having all but the lower back corner sliced off, and you can kind of guess that the hidden center cube will show the hexagon face.
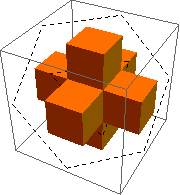
Sure enough, the combination of the exposed inner hexagon and the surrounding exposed triangles makes up the star shape.
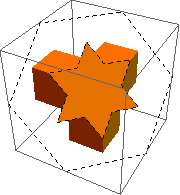
(End of detour.)
If you do the same thing with the next iteration of the Menger sponge, the exposed hexagon surface shows even more star-shaped holes, where the slice meets the different sizes of square holes.

And the next iteration shows even more.

Nice, isn’t it?
Inspired by this page and links: http://www.johndcook.com/blog/2011/08/30/slice-a-menger-sponge/.
Work in progress, but how about this asterisk-shaped hole in a slice through the cross Menger cube?

And again.

Designed and rendered using Mathematica.
© 2014–2026 by Robert Dickau.
[ home ] || [ 2015-01-25 ]