I’m probably doing this wrong, but here goes: Start with a square.

Next, scale down the original square and move copies of it to the four corners of the original square.

Finally, fill in the gaps along the edges with even smaller scaled copies of the squares.

That’s the shape we want. The hole looks kind of like something called a Jerusalem cross—I don’t completely see it myself, looks more like a Greek cross—hence one of the names for the overall figure.
If we choose a scaling factor between the original square and the smaller copies as k = (√2 − 1), and the scaling factor between the original square and the smallest to be k2, since k + k2 + k = 1, each iteration fits in the previous one’s space.
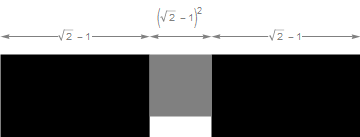
After that, repeat the process of scaling, copying, and translating, and the limiting figure is the Cross Menger square, or Jerusalem square, depending on whom you ask.

I say that I might be doing it wrong because half of the figures out there in the world don’t use just the two different scales with the previous iteration, as here (and the Cube de Jérusalem page on Wikipedia), but instead mix in different scales with the two previous iterations, if that makes sense. For example, see the pages here and here.

In this style, the crosses added at each step are all the same size. Live and let live. Here are inverse figures of the previous, in case you’re interested:

In any case, you can do the same thing in three dimensions: Start with a cube, and then for each iteration make eight smaller copies in the original cube’s corners, and then squeeze in twelve even smaller copies between those. Repeat the process as long as you can stand it, and the limiting figure is the Cross Menger cube, or Jerusalem cube.

Or here’s the other style, if you prefer.

I think these are the complements of the previous, but I’m in kind of a hurry and need to verify later:

The Cross Menger/Jerusalem cube is different from similar-looking fractals such as the Menger sponge in that the ratio between each iteration’s components is an irrational number, (√2 − 1). The Menger sponge pieces, on the other hand, have a (rational) middle ninth punched out each time. Remember when we thought that was cool?
A natural extension is to pick a side length so that s + s2 + s3 + s = 1.
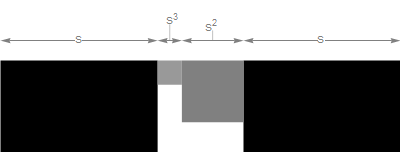
(Previous figure lists the parts in reverse order, if you couldn’t tell.)
That gives us a fractal that looks like a houndstooth pattern:

The 3-D version is disappointing: four of the cube’s sides have nice rotational symmetry, but the other two (look at the right side) are just diagonally symmetric, which ruins the effect. No surprise, since there are three faces but only two sizes of neighbors, but still.
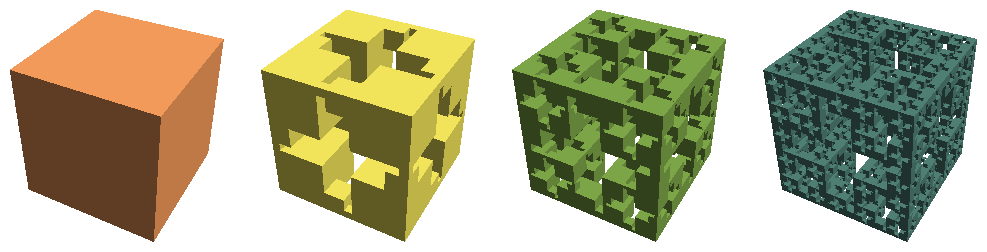
Let’s see where this goes. Here’s an obvious next step of the houndstooth fractal:

Keeping the largest corner copies (size k) in place, the middle parts k2, k3, and k4—in addition to {2,3,4} above—can also be ordered as {2,4,3} and {3,2,4}. Here’s {2,4,3}:

And here’s the vaguely bat-shaped {3,2,4}:

Not much excitement after that. The version with k + k2 + k3 + k4 + k = 1 is awfully similar to the previous version—see those four white dots?

Another hash-sign-like 3-D variant with k + k2 + k + k2 + k = 1.

And their complements.

You might also enjoy Sliced Fractal Sponges or Fractal Sponge Variants.
Designed and rendered using Mathematica.
© 2014–2026 by Robert Dickau.
[ home ] || [ 2025-08-14 ]