
This page is a holding area for miscellaneous variants of fractal carpets and sponges such as the Menger sponge and the Jerusalem/Cross Menger sponge.
For example, here’s one variant of the Sierpinski carpet with non-square holes cut out at each iteration.

And here’s another variant with different scaling factors from the previous set.

This Menger sponge variant is based on Fig. 6.6.3 in Gerald A. Edgar, Measure, Topology, and Fractal Geometry, Springer-Verlag, 1990, p. 187.
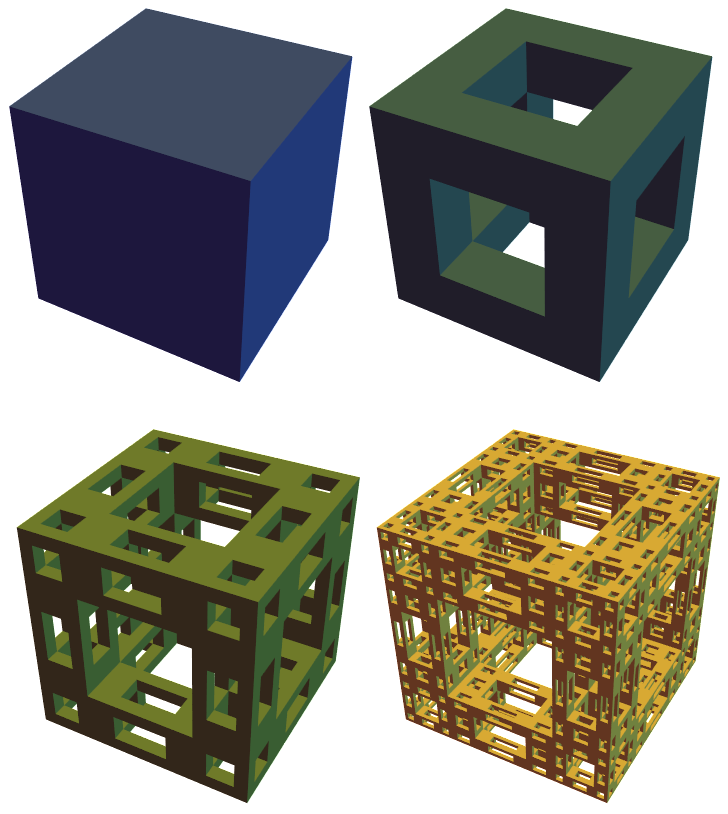

The idea is that the respective iterations are self-affine but not self-similar. Something about calculating the Hausdorff dimension doesn’t work the same way. Gerald A. Edgar labels the figure “Homeomorph of the Menger sponge”.
For that matter, there’s no need for the scales to be symmetric.


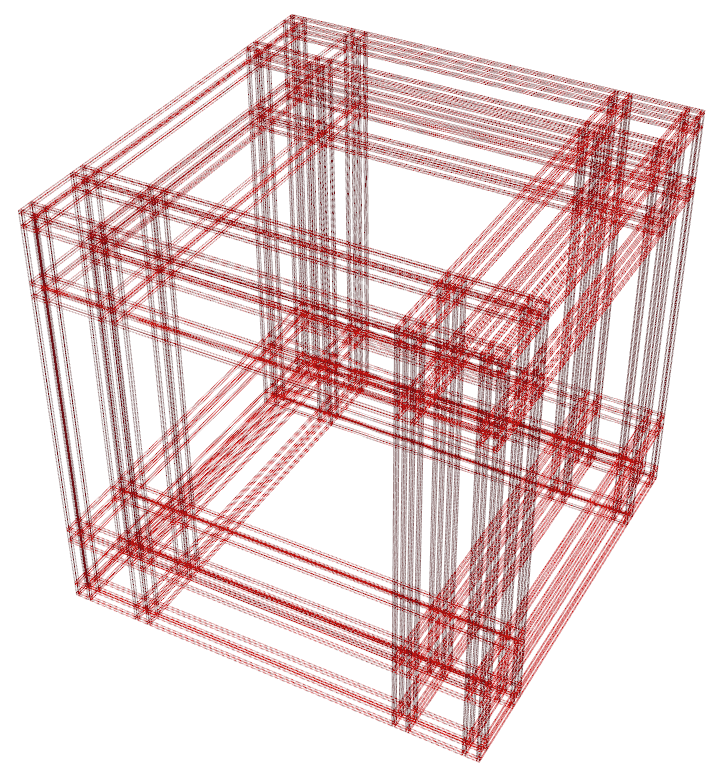
Complements of levels 1, 2, and 3, if you’re interested.

These were first drafts of the previous, before I noticed I’d missed the point.

And here are variations of the Cross Menger (Jerusalem) carpet using a triangle base.




In Kigami and Lapidas’s paper “Weyl’s Problem for the Spectral Distribution of Laplacians on P.C.F. Self-Similar Fractals”, a similar figure (Fig. 2) is called a Modified Sierpinski gasket. (Thanks to Roger Bagula for the reference.)
Ditto, with a tetrahedron base.
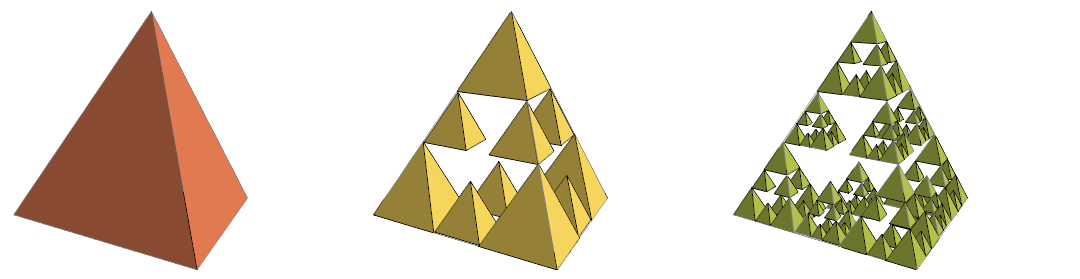

Complements of the previous.

And some lopsided versions of the triangle carpet.

Similar, with interior rotations:

And a rotationally symmetric variant:

Figures created with Wolfram Mathematica versions 10, 11, 12, and 14.
Robert Dickau, 2016–2026.
[ home ] || [ 2025-11-01 ]
robertdickau.com/spongevariants.html