If you weren’t tired of stamp foldings before, this ought to do it. Combining the ideas of unlabeled stamp foldings and symmetric stamp foldings, here are some symmetric unlabeled stamp foldings.
A stack of one stamp is trivially symmetric:
![]()
Both foldings of two stamps are symmetric:
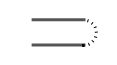
Of the six foldings of three stamps, there’s only one basic shape:
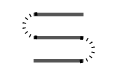
And of the sixteen foldings of four stamps, only two basic shapes:
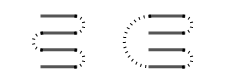
Five stamps, three shapes:
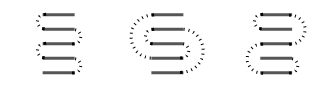
Six stamps, four shapes:

Seven stamps, nine shapes:

Eight stamps, ten shapes:
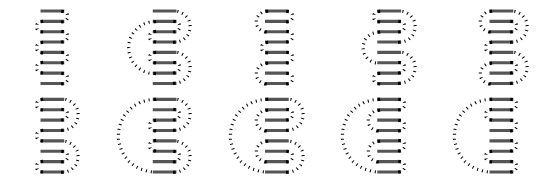
Nine stamps, twenty-eight shapes:
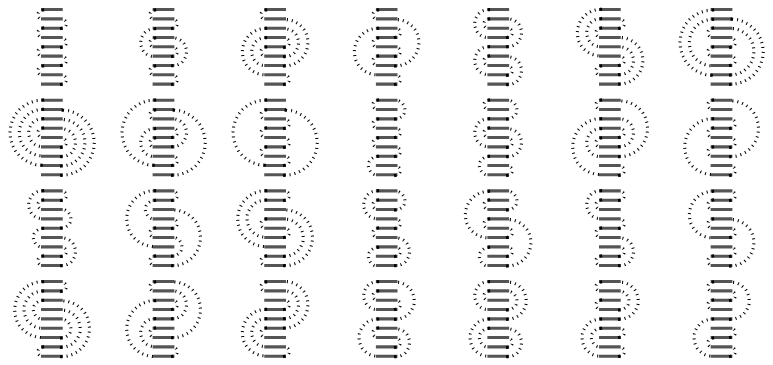
Ten stamps, twenty-four shapes. It’s a little surprising that the count decreases from the nine-stamp case, but that’s the pattern from here on out: the symmetric unlabeled folding counts for a stack containing an even number of stamps increase much more slowly than the counts for stacks containing an odd number of stamps.
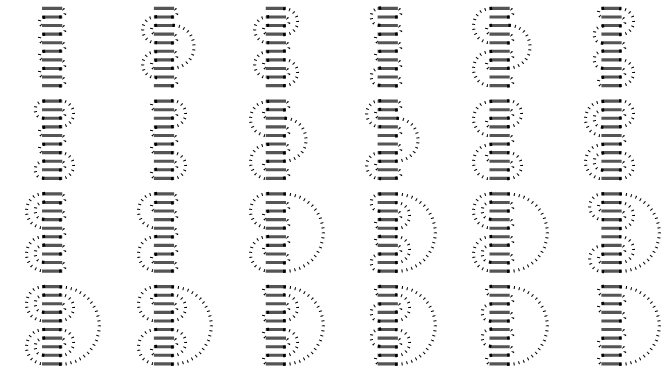
This is OEIS sequence A001010 divided by two (apart from the one-stamp stack).
If you kind of liked this, you’ll kind of love labeled stamp foldings, unlabeled stamp foldings, symmetric stamp foldings, and map foldings.
See Martin Gardner, Wheels, Life and Other Mathematical Amusements, pp. 60–61, 1983.
Figures created with Mathematica 10.
Copyright © 2015–2026 Robert Dickau. All rights reserved, no responsibility accepted.
[ home ] || [ 2016-02-13 ]
www.robertdickau.com/symmetricunlabeledfoldings.html