The Wunderlich curves are a collection of plane-filling curves, similar to the Hilbert and Moore curves. Each Wunderlich curve begins with a seed shape, and each successive iteration translates-rotates-reflects copies of the seed in a 3×3 grid in such a way that the end of one copy is next to the beginning of the next copy.
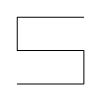
The first type begins with an S-shape, which winds from the southwest corner of its bounding square to end up in the northeast corner:

Copies are arranged in a 3×3 grid, with every other copy being rotated 90 degrees:

And finally the copies are joined in a sort of N-shaped route (up the left column, down the middle column, up the right column):
Repeating the process gives the first type of Wunderlich curve:

The second type begins with the same S-shape, but reflects (instead of rotates) every other S-shape in the grid before joining the copies in the same N-shape order:

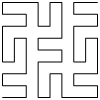
The third type begins with a shape that winds from the southwest corner to the southeast corner, in a kind of R-shape. The copies of the figure are rotated and reflected as need be, and then joined in the same overall R-shaped path:

Like many plane-filling curves, variations of the Wunderlich curve have space-filling analogies in three dimensions. Start with a seed shape:

And then arrange the copies end-to-end-to-end in a 3×3×3 lattice. Here, the top and bottom layers are joined in that N-shaped order, and the center layer is joined in the S-shaped order.
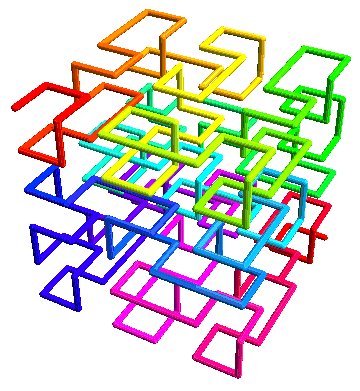
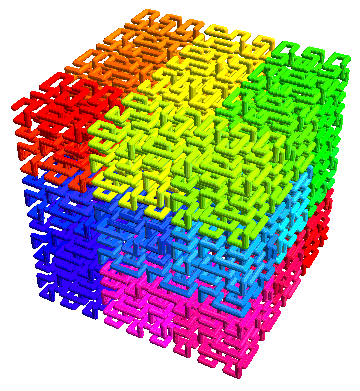
Of course many variations are possible by rotating and reflecting the seed copies in different combinations, along with joining them in different orders, but that’s another story for another time.
See Sagan, Space-Filling Curves, Universitext, 1994, pp. 43–45. Figures created with Mathematica 6.
© 2008–2026 Robert Dickau.
[ home ] || [ 2008-11-19 ]
www.robertdickau.com/wunderlich.html