The number of paths of length 4n from one corner of an n × n × n × n lattice to the opposite corner is
![]() ;
;
the first few values (starting with n = 0) are 1; 24; 2,520; 369,600; 63,063,000; 11,732,745,024; 2,308,743,493,056; 472,518,347,558,400; 99,561,092,450,391,000; 21,452,752,266,265,320,000; 4,705,360,871,073,570,227,520; …. (Compare this to the 2-D and 3-D versions of the same idea.)
There are 24 possible paths of length 4 through a 1 × 1 × 1 × 1 lattice from one corner (0,0,0,0) to the opposite corner (1,1,1,1).

For a 2 × 2 × 2 × 2 lattice*, there are 2,520 paths of length 8 from the green dot (0,0,0,0) to the red dot (2,2,2,2).

Here are the first eight:
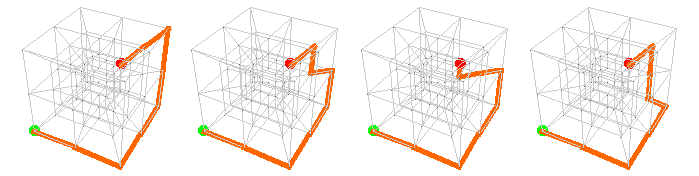
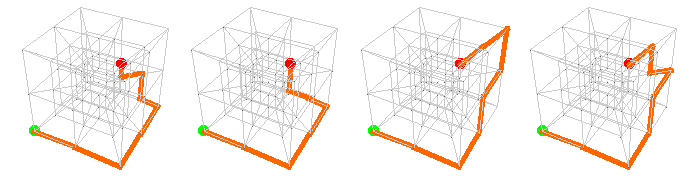
Here is a “middle” path, from (0,0,0,0) to (0,0,0,1) to (1,0,0,1) to (1,1,0,1) to (1,1,0,2) to (2,1,0,2) to (2,2,0,2) to (2,2,1,2) to (2,2,2,2):
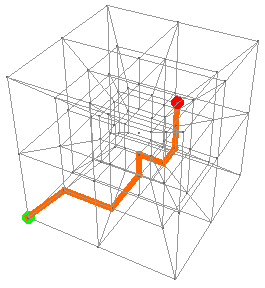
And here are the last eight:
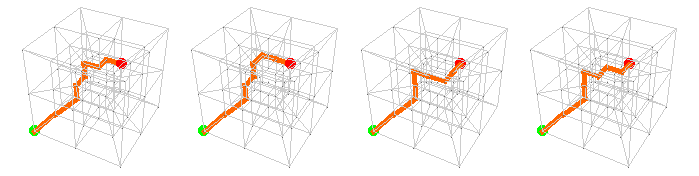
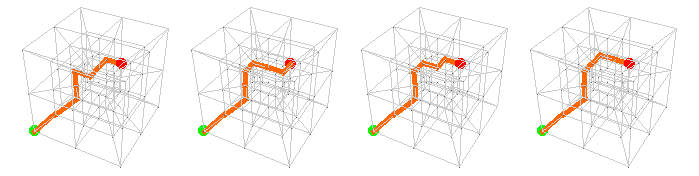
* You’ve surely noticed that the positive x, y, and z axes point in the usual directions, and that the positive w-axis points “inward”; thus w = 0 corresponds to the outer cube, w = 1 the intermediate cube, and w = 2 the inner cube. The trouble is, I had no idea what to do with the points (1, 1, 1, n), so I did nothing: they all map to the unattached point at the center of the whole arrangement. If you have a better idea, please let me know.
© 1996–2026 Robert Dickau
[ home ] || [ 1999-04-06 ]
www.robertdickau.com/path4d.html