Where the Stirling partition numbers S(n, k) describe the number of ways a set with n elements can be partitioned into k disjoint, non-empty unordered subsets, the Lah numbers Ln, k describe the same situation where the contents of the subsets are ordered.
For example, L3, 2 corresponds to partitions of the three elements {A, B, C} into two ordered subsets (the order of the subsets themselves doesn’t matter, though) in these ways:
So L3, 2 = 6. (With the Stirling partition numbers, on the other hand, {A, B} is the same as {B, A}, so removing these “duplicates” gives us S(3, 2) = 3.)
Jumping right in, L2, 1 = 2! = 2. In other words, the set of two items can be “divided” into one ordered subset in these two ways:
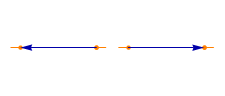
L2, 2 = 1:
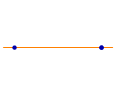
L3, 1 = 3! = 6. (In fact, Ln, 1 is always n!, since the one subset of n items can be ordered in n! ways.)

L3, 2 = 6:

L3, 3 = 1. (Ln, n is always 1, since the n items can be divided into n subsets in only the one way.)
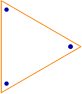
L4, 1 = 4! = 24, about which see permutations.
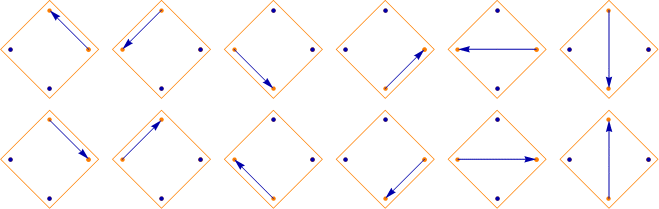
L4, 2 = 36. Of those 36, 24 look like this:

And 12 of them look like this:

L4, 3 = 12:
L4, 4 = 1:
Sums of Stirling partition numbers are the Bell numbers, sums of Narayana numbers are the Catalan numbers, but sums of Lah numbers don’t seem to have a common name.
See Riordan, Introduction to Combinatorial Analysis, New York: Dover Publications, 2002, pp. 43–44.
Designed and rendered using Mathematica 7.0.
© 2011–2026 by Robert Dickau.
[ home ] || [ 2013-09-22 ]