The number of possible paths of length 5n from one corner of an n-by-n-by-n-by-n-by-n lattice to the opposite corner can be calculated using this formula:
![]()
The first few terms are 1, 120, 113400, 168168000, 305540235000, 623360743125120, ... (Compare this to the 2-D, 3-D, and 4-D versions of the same idea.)
The empty 1-by-1-by-1-by-1-by-1 lattice looks like this, where each pair of “adjacent” points is joined by a line, and the starting and ending points are highlighted:
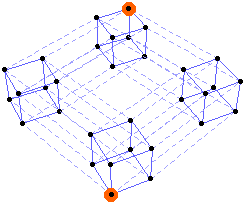
Each step of the path can occur in one of five directions.
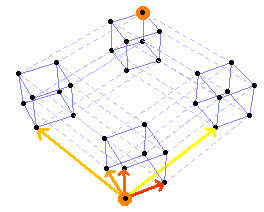
For the 1-by-1-by-1-by-1-by-1 case, we’re counting paths of length 5; since each path will be made up of one step in each of the five directions, we can easily enumerate the paths by computing all the permutations of (dir1, dir2, dir3, dir4, dir5).
For the 1 × 1 × 1 × 1 × 1 lattice, here are the 120 (that is, 5!) paths:

Designed and rendered, at one time or another, using Mathematica for the Apple Macintosh, Microsoft Windows, and for NeXT.
© 1996–2026 Robert Dickau.
[ index ] || [ 2010-12-27 ]
www.robertdickau.com/path5d.html